株や仮想通貨の予測のためには、時系列データの取り扱いが重要です。
今回は、Chainerを用いて時系列データの学習と予測をしてみましょう！

とりあえず試してみたい方は、こちらからすぐに実行可能なノートブックが利用できます！

関連：ニューラルネットでsin波を学習してみよう【Chainer入門】
関連： あなたに最適なpython入門書を見つけよう！

はじめに

この記事では、ニューラルネットワークを用いて「時系列データとして」sin波の学習を行います。

前回の記事ではsin関数そのものの学習を行いましたが、今回は波形の学習を行います。

時系列データの学習と予測は、株や仮想通貨における機械学習でも重要となります。

例えばpybitflyerで収集した取引データから、次の一時間の動きを予測するなどの応用が考えられます。

 

ご自身で予測プログラムを組みたいという野心的な方は、ぜひこの記事で時系列データの学習と予測についての基礎を学びましょう！

 

時系列データとは

時系列データとは、時刻に伴って値が変化するようなデータを指します。

例えば株などの値動きや、車の軌道などは時系列データということができます。

これらの動きを予測するためには、直前にどのような動きをしていたかが重要になります。

株や仮想通貨であれば、直前まで値が下がり続けているのであれば、今後もしばらくは下がり続けることが予想されます。

あるいは一定の幅で値が揺れているのであれば、今後もしばらくは同様に揺れることが考えられます。

 

問題設定

今回は時系列データの例として、sin波を用います。

sin関数は入力xについて周期的な値を返す関数ですが、この波が時刻ごとに移り変わる値とみなすことで、時系列データと考えることができます。

 

この記事では直前のsin波の動きを入力として、次の値を予測するニューラルネットワークを構築します。

前回はsin関数の入力xから出力yを予測していたのに対し、今回は直前のyの値のみから予測を行うことに注意してください。

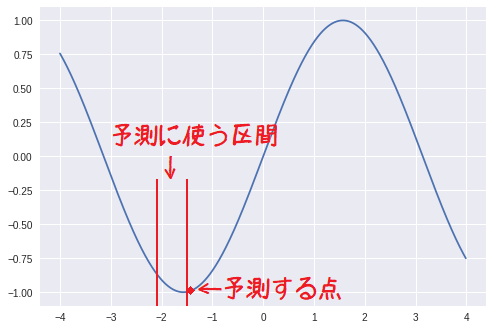
具体的には図のように、直前の時系列データから次の値を予測します。

図では赤い線に挟まれた区間のデータから、赤◆の点を予測する様子を表しています。

 

データ

今回の題材はsin波ですが、前回とは設定が違うため学習用データセットの作り方が異なります。

import numpy as np

# -4.0 ~ 4.0の区間を0.01刻みで800点
sinIn = np.arange(-400,400)*0.01
sinOut = np.sin(sinIn)

# 直前30timeから次を予測する
contextSize = 30
xs = []
ts = sinOut[contextSize+1:]
for i in range(0,sinOut.shape[0]-contextSize-1):
  xs.append(sinOut[i:i+contextSize])
  
xs = np.array(xs,'f')
ts = np.array([ts],'f').T

前回同様、sin波を0.01刻みで800分割し、これを用いて学習ようデータを作成します。

上で紹介した図のように、予測に使うデータをx、予測する点をtとしてデータを作ります。

今回は直前の30時刻から、次の点を予測するようにデータを作成しました。

 

モデル

今回用いるモデルは、直前の30個の値を横に並べた横ベクトルを線形層によって予測値に飛ばすものです。

つまり、入力は30次元のベクトルで、出力が1次元のスカラになります。

途中で一度50次元のベクトルに写すことで、表現力を高めています。

 

### 予測モデルの構築 ###
import chainer
from chainer import Chain
from chainer import functions as F
from chainer import links as L
class Model(Chain):
  def __init__(self, contextSize, hidSize=30):
    super().__init__()
    linear1 = L.Linear(contextSize, hidSize)
    linear2 = L.Linear(hidSize, 1)
    
    self.add_link('linear1',linear1)
    self.add_link('linear2',linear2)
    
  def forward(self, contexts):
    hs = F.tanh(self.linear1(contexts))
    ys = self.linear2(hs)
    return ys

 

学習

クラスの宣言

前回同様、学習に用いるモデルと最適化に用いるオプティマイザを宣言します。

最適化にはAdamと呼ばれる手法を用います。

# モデルの準備
from chainer import optimizers
model = Model(contextSize)
opt = optimizers.Adam()
opt.setup(model)

 

train関数

学習部分は前回と全く同じものを用います。

損失関数は最も単純に二乗誤差を用います。

 

# 学習イテレーション
def train(startEpoch=0, endEpoch=100):  
  losses = []
  for i in range(startEpoch, endEpoch):
    model.cleargrads()
    ys = model(xs)
    loss = F.average(F.squared_error(ys,ts))
    loss.backward()
    opt.update()
    losses.append(loss.data)
  plt.plot(list(range(startEpoch, endEpoch)),losses, label='loss')
  plt.legend()

 

eval関数

モデルの評価は、波形の再生成によって行います。

具体的には、用意したsin波の最初の30時刻を用いて次の点を予測し、予測した点を用いてさらに次を予測する、といった具合に生成を行います。

# timeStep回の生成で評価
def evaluate(initialContext=xs[[0]]):
  timeStep = len(ts)
  ys = initialContext
  for t in range(timeStep):
    y = model(ys[:,-contextSize:])
    ys = np.hstack([ys,y.data])
  ys = ys[0,contextSize:]
  plt.plot(ys,label='predict')
  plt.plot(ts,'r',label='gold')
  plt.legend()

 

本来の波形を重ねることで、生成結果がどれほど本来の波形とずれているかを確認することができます。

この評価方法では、自分が生成した値を用いて次の点を予測するため、自分自身の間違いによってどんどん出力がずれてしまいます。

しかし、学習を重ねることっで比較的マシに波形を復元できるようになります。

 

実験

では実際にモデルを学習し、波形の生成を行ってみましょう。

学習なし

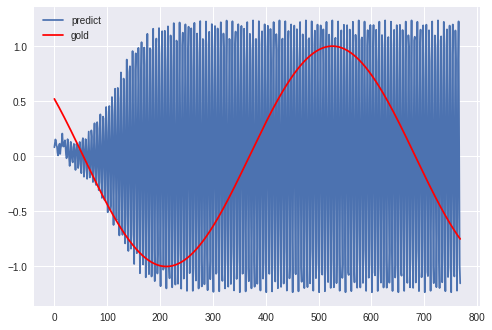
まず、学習を行っていないモデルによる予測結果を載せます。

青線がモデルによる予測、赤線が実際のsin波です。

図のように、周期的ではありますが全くフィットしていません。

 

1000エポックの学習

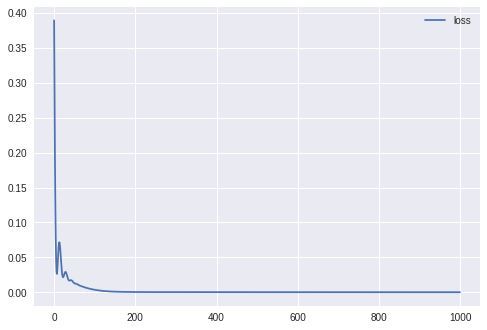
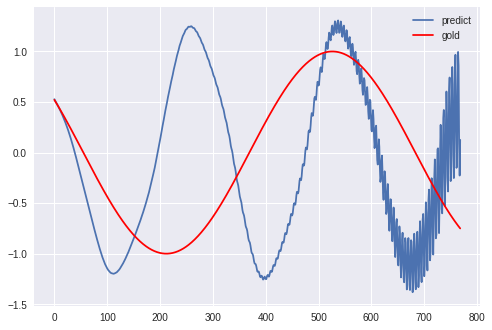
今回もロスの変化と評価結果を載せていきます。

まず最初に大きくロスが下がり、徐々にフィットしていきます。

1000エポックの学習が終わった時点で、ある程度波形は再現できていますが、後半になるにつれてだんだんと揺れが激しくなっています。

また、実際のsinカーブよりも周期が短くなっていますが、これは自分自身が生成した予測を用いて次を予測しているために生じるズレです。

 

 

10000エポックの学習

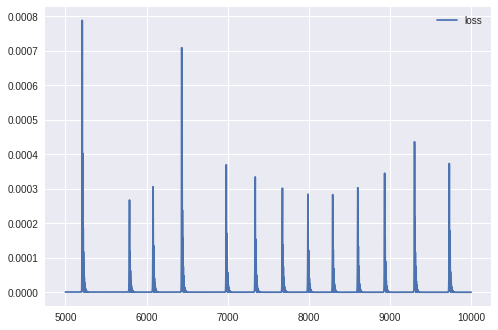
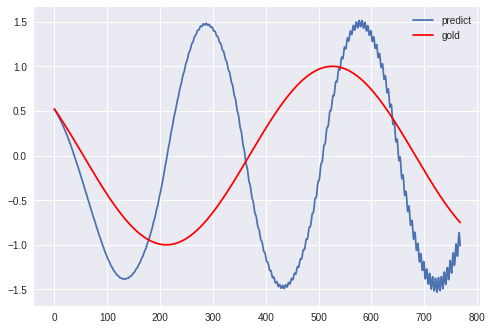
1000~5000エポックの様子は飛ばし、10000エポックが終わった時点での結果を見てみましょう。

途中経過はノートブックから確認できますので、興味がある方はご覧ください。

10000エポックの学習によって、後半の揺れがだんだん小さくなっていることが確認されます。

 

20000エポックの学習

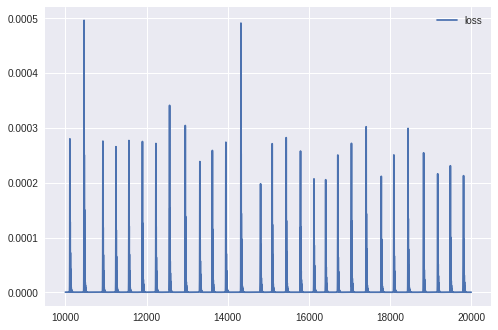
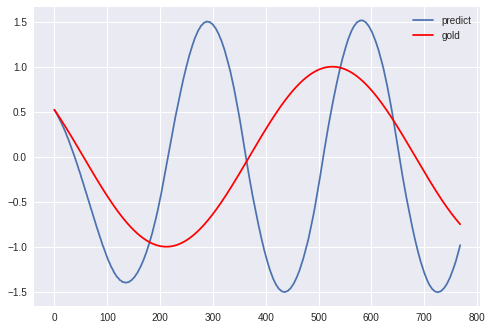
さらに学習を進めることで、後半の揺れは完全に収まりました。

しかし、実際のsinカーブよりも周期が短いという点は改善されていません。

また、実際の波形よりもかなり波の高さが大きいこともわかります。

 

時系列データ学習の難しさ

そもそもの難しさ

実験で見た通り、今回のモデルではsin波を完全に再現できていません。

時系列データは自分自身の出力を信じて次を予測するという点において、難しさがあります。

これは今回用いたモデルが単純であるということにも起因しますが、やはり時系列データそのものが難しい問題設定であるということの方が大きな原因です。

 

初期値の難しさ

また、モデルのパラメータの初期値によって全く学習ができないことがあるのも、今回ご紹介したモデルの難しさです。

初期値で以下のような波形を生成するモデルについて学習を行います。

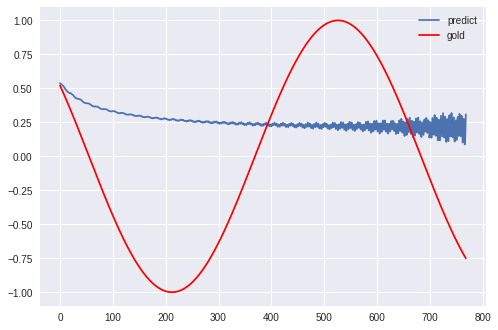
これをどれだけ学習しても、なかなかうまく波形が再現されません。

具体的に、20000エポックの学習を行うと、以下のような波形が生成されます。

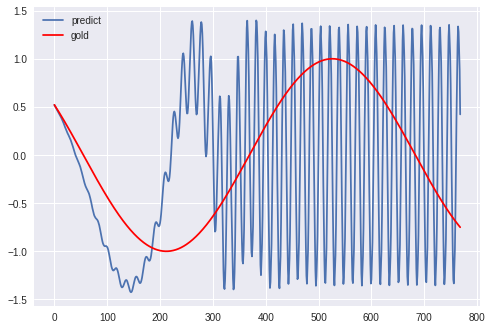
このように、なかなか学習ができず、波形の再現もできていません。

初期値への依存はニューラルネットワークの大きな問題ですが、このような単純な課題を通しても、この問題を確認することができます。

 

まとめ

今回はニューラルネットワークを用いて、時系列データとしてsin波を学習する方法をご紹介しました。

実験で見た通り時系列データの学習は難しく、なかなか再現できないこともよくあります。

しかし、時系列データの予測は難しいだけにやりがいがあるテーマだとも言えます。

次回は時系列データを用いるために提案されている、ニューラルネットワークの優秀なモデルを用いた予測をご紹介します！