Chainerを用いて単純なニューラルネットワークを構築し、sin波を学習してみましょう！

とりあえず試してみたい方はこちらからすぐに実行可能なコードに触れることができます！

関連：ニューラルネットで時系列データを学習しよう【Chainer入門】
関連： あなたに最適なpython入門書を見つけよう！

 

はじめに

この記事では、単純なニューラルネットを用いてsin波の学習を行います。

今回使用したコードはGoogle Colaboratoryにて公開しており、こちらから実行できます。

playgroundモードに写すことで実際に実行し、試してみることができます。

以下では上のコードについての解説を行います。

 

前提

この記事ではニューラルネットの構築にChainerを使用します。

また数値計算ライブラリのnumpyも使用します。

上で紹介したNotebookを使用せず、ご自身のパソコンで実験する場合には、以下の手順で必要なライブラリをインストールしてください。

$ pip install numpy
$ pip install chainer

 

データ

今回はsin波を学習するニューラルネットを作り、実験を行います。

-4.0から4.0の区間で0.01刻みの数値xを用意し、それに対応するsin関数の値t=sin(x)を学習するデータとします。

import numpy as np

# -4.0 ~ 4.0
xs = np.arange(-400,400)*0.01

# shuffle
np.random.shuffle(xs)

splitPoint = int(len(xs)*0.9)

# training and test inputs
xsTrain = xs[:splitPoint]
xsTest = xs[splitPoint:]

# trainin and test golds
tsTrain = np.sin(xsTrain)
tsTest = np.sin(xsTest)

xsはシャッフルされた-4.0から4.0の値です。

splitPointはデータを9:1に分割するための変数で、データの90%を学習、10%をテストに用います。

xsTrain,とtsTrainは学習に用いる入力と教師データで、xsTestとtsTestはテストに用いる入力と正解データです。

ここで入力とは、ニューラルネットへの入力を指します。

 

用意した学習用データとテスト用データは以下のグラフのようになっています。

横軸が入力で、対応する教師データが縦軸です。

青が学習に用いるデータ、赤がテストに用いるデータです。

 

さらにニューラルネットに食わせやすくするため、データの向きを変えます。

また、Chainerではfloat32を使用する必要があるため型を変換しておきます。

これらの処理はニューラルネットについて本質的ではないため、理解は後回しで構いません。

# 使いやすいようにデータの向きを変えておく
xsTrain = np.expand_dims(xsTrain,axis=1)
xsTest = np.expand_dims(xsTest,axis=1)
tsTrain = np.expand_dims(tsTrain,axis=1)
tsTest = np.expand_dims(tsTest,axis=1)

# chainerではfloat32を使う
xsTrain = xsTrain.astype('float32')
xsTest = xsTest.astype('float32')
tsTrain = tsTrain.astype('float32')
tsTest = tsTest.astype('float32')

 

モデル

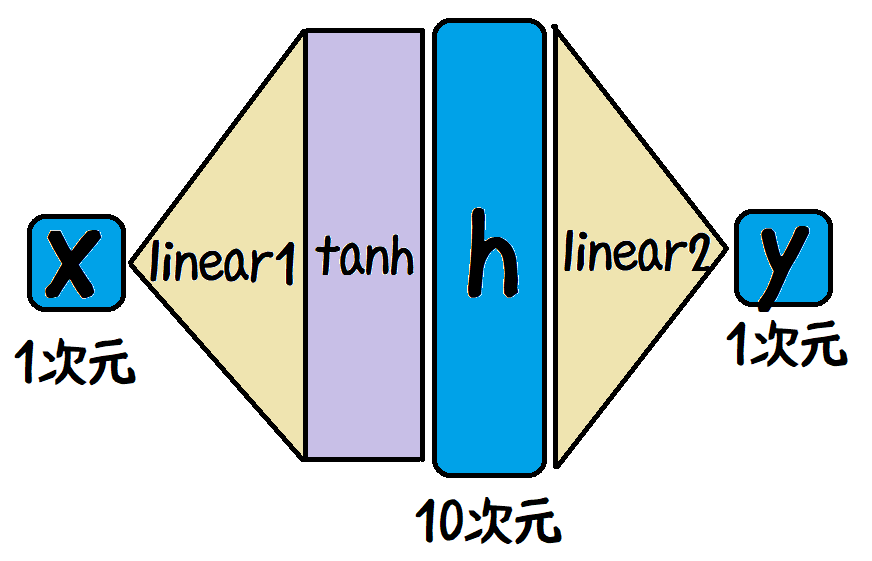
今回用いるモデルのイメージを上に示しました。

ここでxはニューラルネットへの入力、yはニューラルネットによる出力です。

青色の丸角四角はベクトル、ベージュの三角は線形層、紫の四角は非線形関数です。

詳細な説明は省きますが、1次元の入力をより表現力の高い10次元に写したのち、再度1次元に戻すというイメージをつかんでください。

 

これをChainerで書くと以下のようになります。

from chainer import Chain
from chainer import links as L
from chainer import functions as F
class Model(Chain):
  def __init__(self, hidSize=10):
    super().__init__()
    linear1 = L.Linear(1,hidSize)
    linear2 = L.Linear(hidSize,1)
    self.add_link('linear1',linear1)
    self.add_link('linear2',linear2)
  
  def forward(self, xs):
    hs = F.tanh(self.linear1(xs))
    ys = self.linear2(hs)
    return ys

入力はxの値、出力は対応するsin(x)ですので、入力出力ともに次元数は1です。

これを線形層(linear1)によって一度10次元にしたのちに、異なる線形層(linear2)によって1次元に戻します。

 

学習

クラスの宣言

# モデル宣言
model = Model()

# optimizer宣言
from chainer import optimizers
opt = optimizers.Adam()
opt.setup(model)

上で定義したモデルを用いるために、まずはモデルを宣言します。

また、学習を行うためにOptimizerを設定します。

詳しくは省略しますが、ニューラルネットワークによる予測値と、正解の数値（教師データ）との誤差が小さくなるように学習を行うものだと考えてください。

 

train関数

上で宣言したモデルを学習するための関数を書きます。

def train(startEpoch=0, endEpoch=100):  
  for i in range(startEpoch, endEpoch):
    model.cleargrads()
    ys = model(xsTrain)
    loss = F.average(F.squared_error(ys,tsTrain))
    loss.backward()
    opt.update()

各エポックにおいて、xsTrainをニューラルネットに入力し、その出力ysと教師データtsTrainとの二乗誤差を最小化します。

今回は二乗誤差を用いていますが、この値は「ロス」と呼ばれ、ロスを最小化するようにニューラルネットのパラメーターを更新することで、「学習」を行います。

 

evaluate関数

また、学習済みのモデルをテストデータで評価するための関数が必要です。

ほとんどtrain関数と同じですが、学習を行わずに二乗誤差の結果だけを表示しています。

（ノートブックでは結果をグラフにプロットするようになっています。）

def evaluate():
  ys = model(xsTest)
  # loss
  print('average loss', F.average(F.squared_error(ys,tsTest)))
  
  # show
  plt.scatter(xsTest, ys.data, color='blue')
  plt.scatter(xsTest, tsTest, color='red')

 

 

実験

最後に、作成したニューラルネットを用いて実験を行います。

各エポックの学習時点でのロスの下がり方と、テストデータに対する予測値をグラフでお見せします。

1~100 epoch

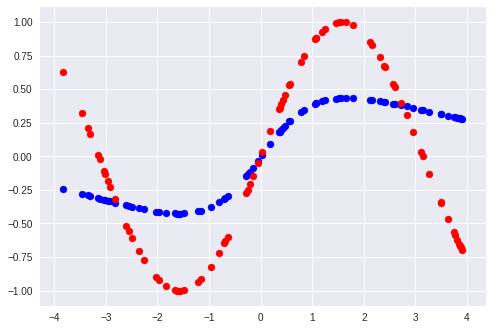
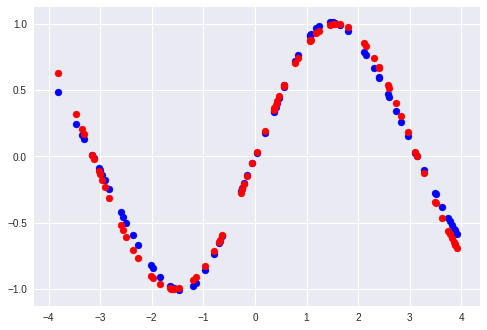
100 epochまでのロスの遷移と、予測に対する正解データのプロットです。

プロットは青が予測、赤が正解となっています。

100エポック程度ではあまり学習ができていません。

同様にして残りの学習結果も見てみましょう。

 

100~1000 epoch

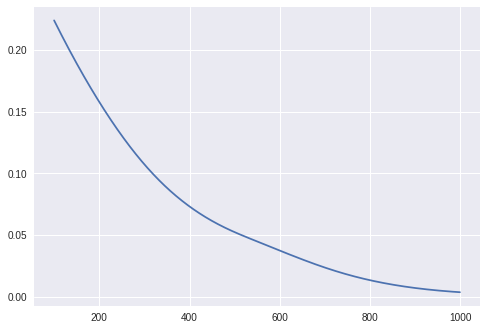
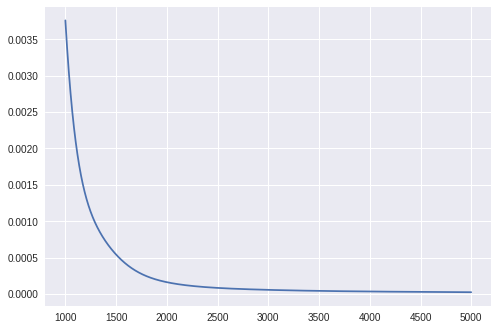
順調にロスが下がり、テストへの結果もフィットしてきています。

 

1000~5000 epoch

5000エポックほどでほとんどロスは収束し、学習が完了した状態になります。

予測もほとんど正解と差がありません。

 

5000~10000 epoch

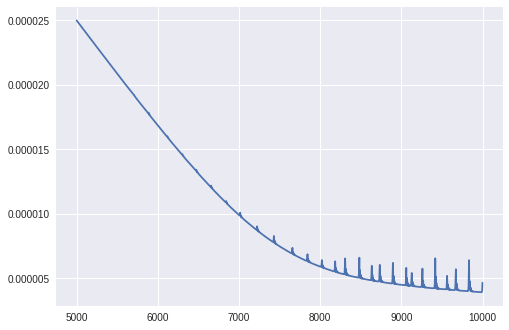
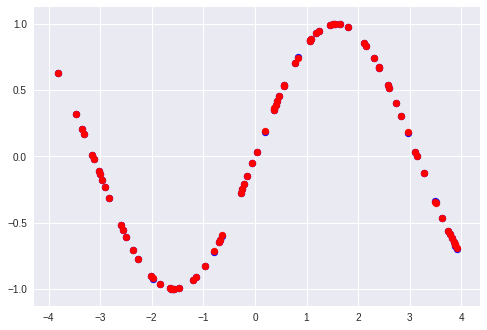
さらに学習を続けると、ロスにトゲのようなものが見られる変化が現れます。

これはニューラルネットの学習においてみられる学習過程で、ロスが下がる前に一度ロスが大きく上がる現象です。

 

今回は詳しく踏み込まないことにしますが、このように「壁を乗り越えてよりロスを下げる学習ができる」ことが、ニューラルネットの強みと言えます。

 

まとめ

この記事ではChainerを用いてsin波の学習実験を行いました。

単純な構造のため、ニューラルネットワーク自体の勉強にもなる題材です。

ぜひ皆さんも試してみて、ニューラルネットへの理解を深めましょう！

関連：ニューラルネットで時系列データを学習しよう【Chainer入門】